문제
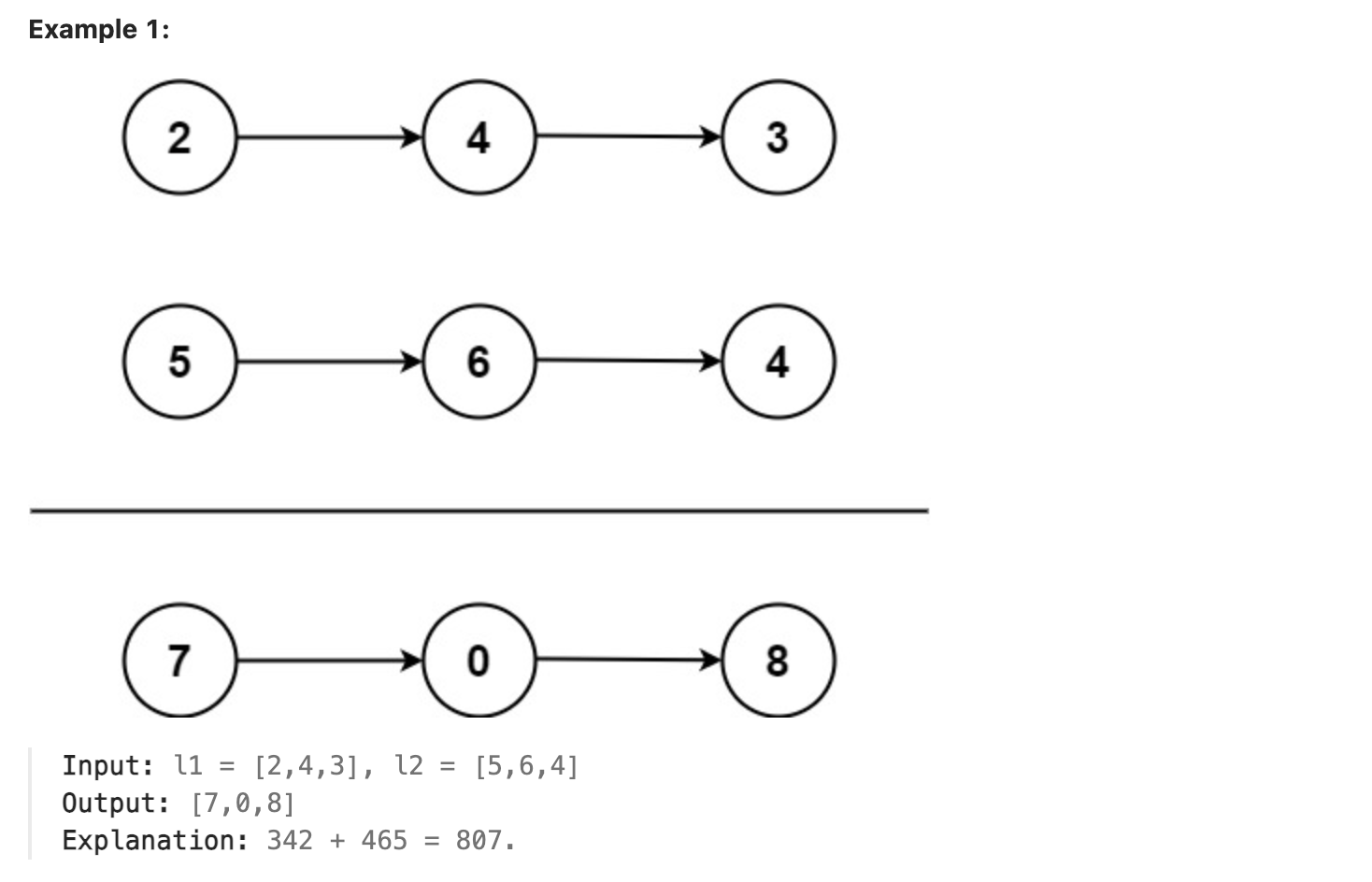
역순으로 저장된 연결 리스트의 숫자를 더하라.
입력
1
(2 -> 4 -> 3), (5 -> 6 -> 4)
출력
1
7 -> 0 -> 8
설명
342 + 465 = 807
풀이 1 (자료형 변환)
입력으로 들어오는 두 리스트를 역순으로 된 연결리스트로 변환 후 두 리스트를 더해야 한다. 역순으로 리스트를 변환하는 코드는 다음과 같다.
1
2
3
4
5
6
7
8
9
# 연결 리스트 뒤집기
def reverseList(self, head: ListNode) -> ListNode:
node, prev = head, None
while node:
next, node.next = node.next, prev
prev, node = node, next
return prev
역순으로 연결하기 위해 node.next를 이전 prev 리스트로 계속 연결하면서 끝날 때까지 반복한다. node가 None이 될 때, prev는 뒤집힌 연결 리스트의 첫 번째 노드가 된다.
이 후 덧셈을 위해 연결 리스트를 파이썬의 리스트로 변경해야 한다.
1
2
3
4
5
6
7
# 연결 리스트를 파이썬 리스트로 변환
def toList(self, node: ListNode) -> List:
list: List = []
while node:
list.append(node.val)
node = node.next
return list
node를 list에 삽입하면서 변환하는 코드이다.
덧셈 후 다시 역순으로 된 연결 리스트로 변환해야 되기 때문에 리스트를 역순 연결 리스트로 변환하는 코드는 다음과 같다.
1
2
3
4
5
6
7
8
9
# 파이썬 리스트를 연결 리스트로 변환
def toReversedLinkedList(self, result: str) -> ListNode:
prev: ListNode = None
for r in result:
node = ListNode(r)
node.next = prev
prev = node
return node
역순 연결리스트로 변환 해주는 함수에서 매개변수가 str 인 result변수로 받게되는데, 이는 덧셈 풀이에서 문자열로 변환해서 작업했기 때문이다. 덧셈 코드를 보면 다음과 같다.
1
2
3
4
5
a = self.toList(self.reverseList(l1))
b = self.toList(self.reverseList(l2))
resultStr = int(''.join(str(e) for e in a)) +
int(''.join(str(e) for e in b))
입력받은 두개의 리스트를 역순 연결 리스트로 변환하고 파이썬의 리스트로 변경 후, 덧셈 연산을 위해 리스트를 int형태로 결합해여 한다. 그러기 때문에 합치기 전에 문자형으로 먼저 변경이 필요하다.
1
int(''.join(str(e) for e in a))
여기서 str(e) 로 각 항목을 문자로 변경한 다음 join()으로 합쳤다. 합치고 난 후 덧셈 연산이 필요하므로 int() 를 이용해 숫자형으로 변환 후 덧셈을 수행한 것이다.
이후, 최종적으로 나온 결과를 역순으로 구성된 연결리스트로 바꾸면 되기 때문에 앞서 작성한 toReversedLinkedList() 를 사용하여 변환해주면 된다.
전체 코드는 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 연결 리스트 뒤집기
def reverseList(self, head: ListNode) -> ListNode:
node, prev = head, None
while node:
next, node.next = node.next, prev
prev, node = node, next
return prev
# 연결 리스트를 파이썬 리스트로 변환
def toList(self, node: ListNode) -> List:
list: List = []
while node:
list.append(node.val)
node = node.next
return list
# 파이썬 리스트를 연결 리스트로 변환
def toReversedLinkedList(self, result: str) -> ListNode:
prev: ListNode = None
for r in result:
node = ListNode(r)
node.next = prev
prev = node
return node
# 두 연결 리스트의 덧셈
def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
a = self.toList(self.reverseList(l1))
b = self.toList(self.reverseList(l2))
resultStr = int(''.join(str(e) for e in a)) + \
int(''.join(str(e) for e in b))
# 최종 계산 결과 연결 리스트 변환
return self.toReversedLinkedList(str(resultStr))
풀이 2 (전가산기 구현)
이번에는 논리 회로의 전가산기(Full Adder)와 유사한 형태로 구현해보자. 이진법이 아니라 십진법이라는 차이만 있을 뿐 자리올림수(Carry)를 구하는 것까지 가산기의 원리와 거의 동일하다. 여기서는 연산 결과로 나머지(Remainder)를 취하고 몫은 자리올림수 형태로 올리는 전가산기의 전체적인 구조만 풀이한다.
1
2
3
4
5
6
7
8
9
sum = 0
# 두 입력값의 합 계산
if l1:
sum += l1.val
l1 = l1.next
if l2:
sum += l2.val
l2 = l2.next
이 코드는 먼저 두 입력값의 합을 구한다. 두 입력값의 연산을 수행하고 다음과 같이 자릿수가 넘어갈 경우 자리올림수를 저장하는 코드는 다음과 같다.
1
2
# 몫(자리올림수)과 나머지(값) 계산
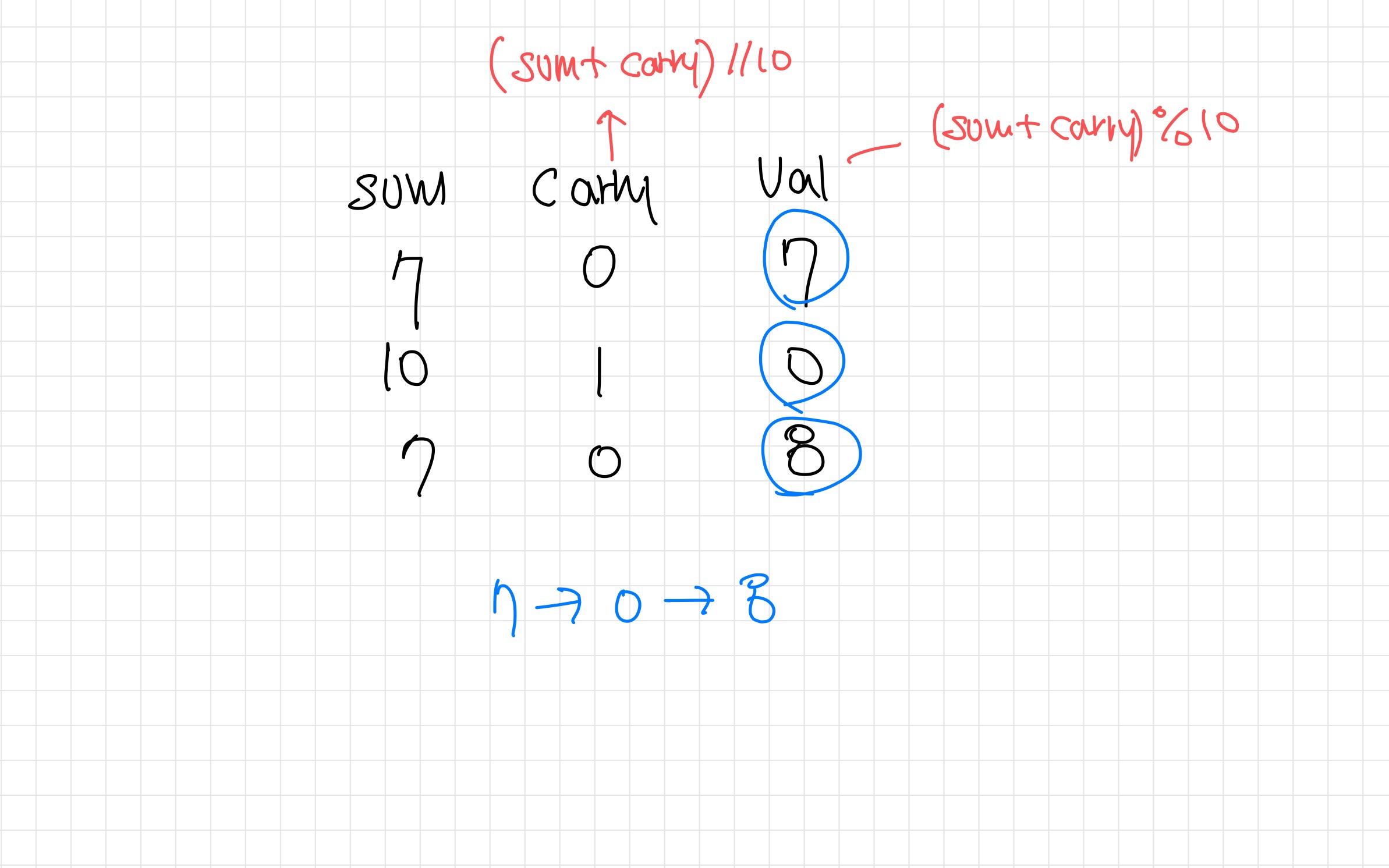
carry, val = divmod(sum + carry, 10)
자리올림수는 파이썬의 내장함수인 divmod() 를 사용하여 구한다. divmod()는 몫과 나머지로 구성된 튜플을 return한다. 즉, (a // b, a % b)와 동일한 결과를 출력한다. 위의 예제를 전가산기 형태로 구현했을 때 sum, carry, val의 변화량은 다음과 같다.
자리올림수(carry)를 설정하여 두 값을 합한 결과가 두 자릿수가 될 경우를 다음번 연산에 사용하고, 나머지는 값을 취하여 이 값을 연결리스트로 만들어주면 된다.
전체 코드는 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
root = head = ListNode(0)
carry = 0
while l1 or l2 or carry:
sum = 0
# 두 입력값의 합 계산
if l1:
sum += l1.val
l1 = l1.next
if l2:
sum += l2.val
l2 = l2.next
# 몫(자리올림수)과 나머지(값) 계산
carry, val = divmod(sum + carry, 10)
head.next = ListNode(val)
head = head.next
return root.next
정리
연결 리스트를 파이썬의 리스트 형태로 변환하여 풀이하는 방법과 전가산기의 원리와 유사하게 자리올림수를 적용해서 풀이해보았다. 첫 번째 풀이 방법에서 자료형을 일일이 변환하여 풀이하여 코드가 다소 길지만, 두 번째 전가산기 원리를 이용하여 구현했을 때의 코드는 한결 깔끔하다.