탐욕 알고리즘(Greedy Algorithm)이란?
Greedy는 탐욕스러운, 욕심 많은 이라는 뜻이다. 탐욕 알고리즘은 현재 상황에서 지금 당장 좋은 것만 고르는 방법만 의미한다. 그리디 알고리즘 문제로 유명한 거스름돈 문제를 보면서 이해해 보자.
문제
1
2
3
당신은 음식점의 계산을 도와주는 점원이다. 카운터에는 거스름돈으로 사용할 500원, 100원, 50원,
10원짜리 동전이 무한히 존재한다고 가정한다. 손님에게 거슬러 줘야 할 돈이 N원일 때 거슬러 줘야 할 동전의
최소 개수를 구하라. 단, 거슬러 줘야 할 돈 N은 항상 10의 배수이다.
위의 문제는 가장 큰 화폐 단위부터 돈을 거슬러 500원, 100원, 50원, 10원짜리 동전을 차례대로 거슬러 줄 수 있을 만큼 거슬러 주면된다.
1
2
3
4
5
6
7
8
9
n = 1260
count = 0
# 큰 단위의 화폐부터 차례대로 확인
coin_types = [500, 100, 50, 10]
for coin in coin_types:
count += n//coin
n%=coin
위 거스름돈 문제를 보듯이 그리디 알고리즘은 현재 상황에서 가장 좋은 것을 선택해나가는 방식이다. 그러면 이 알고리즘의 방식이 항상 최적의 해를 보장할 수 있을까? 그렇지 않다. 처음에 그리디 알고리즘 문제를 풀어보면서 현재 상황에서 가장 좋은 것만 선택해서 풀려고 하는데, 이 방법이 적용되지 않는 문제들이 많자 왜 그런지 생각해보니 그리디 알고리즘은 미래 상황을 고려하지 않아 전체 문제에서의 최적의 해를 구할 수 없었던 것이다.
현재의 최적해 ≠ 전체의 최적해
그래서 그리디 알고리즘은 최적의 해가 보장된 조건에서만 적용해야되는 알고리즘이다!
그리디 알고리즘 최적의 해 보장조건
1. 현재의 선택이 미래의 선택에 영향을 주지 않는다.
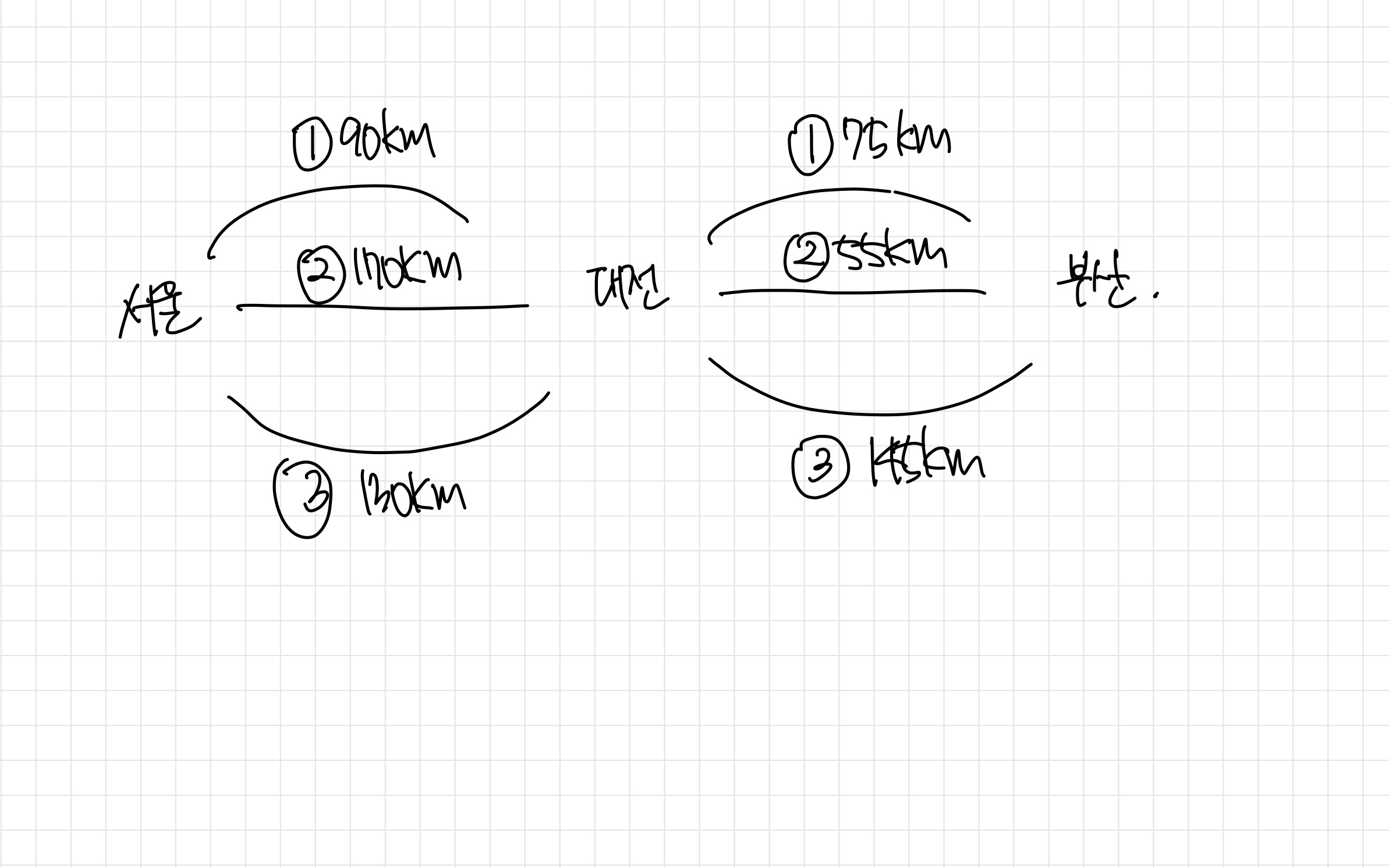
예를 들어 서울에서 부산까지의 최소비용을 구하라고 할때 서울에서 대전까지 가는 경로를 선택하는데 대전에서 부산까지의 경로를 선택하는데 영향을 미치지 않으므로, 서울에서 대전까지 가는 3개의 경로 중 가장 짧은 경로를 택하면 된다. 즉, 현재 선택이 미래 선택에 영향을 주지 않는다. 이럴 때 서울에서 대전까지 가는 비용만 고려하여 선택해도 최적의 해가 보장된다. 이 조건을 탐욕스러운 선택 조건(Greedy Choice Property) 라고 부른다.
2. 부분의 최적해가 모이면 전체의 최적 해가 된다.
위의 같은 문제로 예를 들면 서울에서 부산까지의 최소비용을 구할 때, 이 문제를 쪼개면 서울 → 대전, 대전 → 부산 의 최소 비용을 구하면 된다. 즉, 하나의 큰 문제를 여러개의 작은 문제들로 나눌 수 있고, 그 작은 문제들에 대한 최적의 해가 더해지는 것이 전체 문제의 최적해가 된다. 이 조건을 최적 부분 구조 조건(Optimal Substructure)이라고 한다.