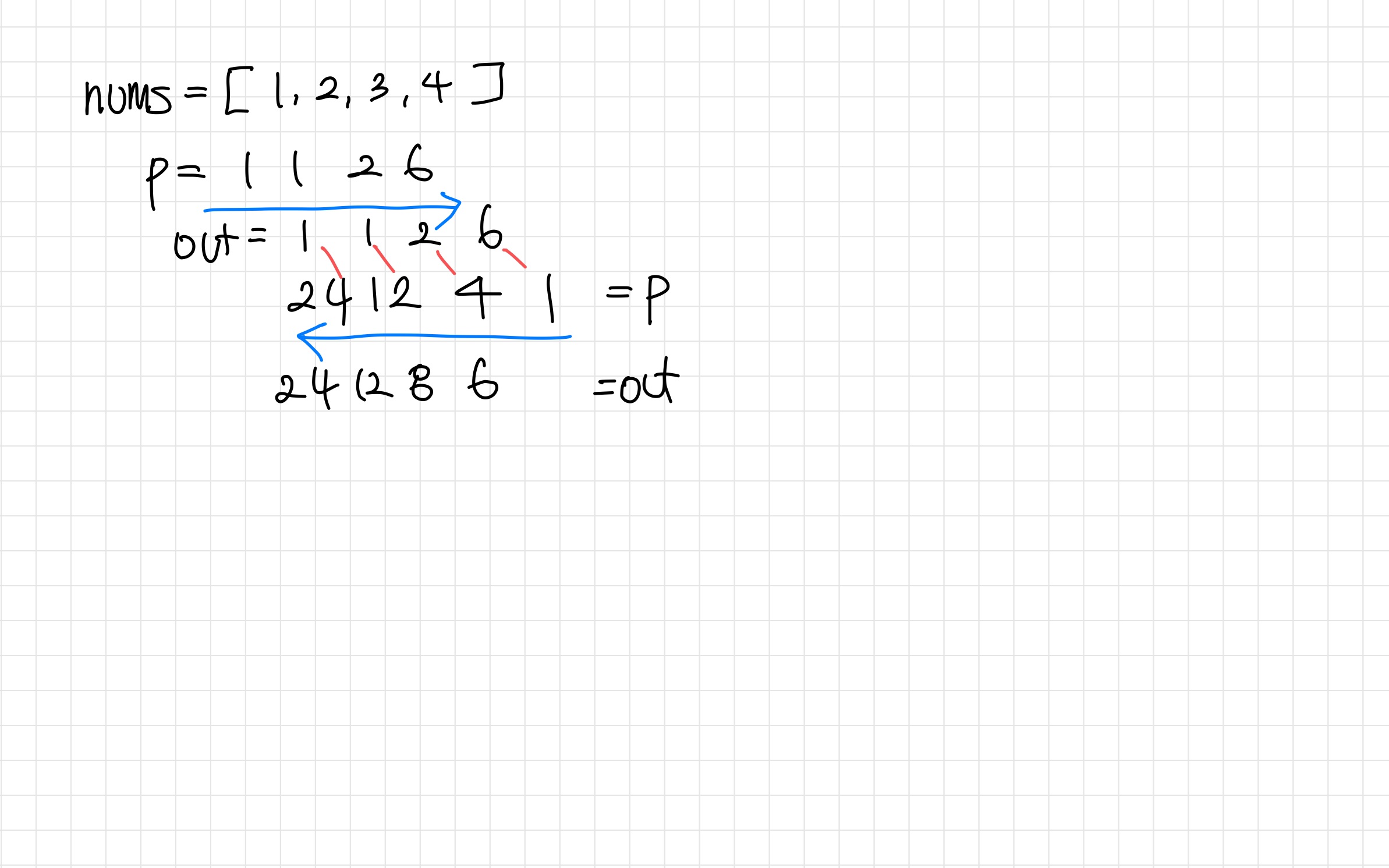문제
배열을 입력받아 output[i]가 자신을 제외한 나머지 모든 요소의 곱셈 결과가 되도록 출력하라. (단, 나눗셈을 사용하지 않고 O(n)에 풀이하라)
입력
1
[1,2,3,4]
출력
1
[24, 12, 8, 6]
풀이 (왼쪽 곱셈 결과에 오른쪽 값을 차례대로 곱셈)
이 문제의 제약사항인 나눗셈을 사용하지 않고 O(n)에 풀이하라고 했는데, 이는 전체 곱셈을 하고나서 각 항목별로 자기 자신을 나눠서 풀이하지 말라는 뜻이다. 그러면 자기 자신을 제외하고 왼쪽의 곱셈 결과와 오른쪽의 곱셈 결과를 곱하면 된다.
먼저 왼쪽부터 차례대로 곱해서 p=1로 시작하여 out 리스트 변수에 담아 결과는 [1,1,2,6]이 된다. 코드는 아래와 같다.
1
2
3
4
5
6
7
out = []
p = 1
# 왼쪽 곱셈
for i in range(0, len(nums)):
out.append(p)
p = p * nums[i]
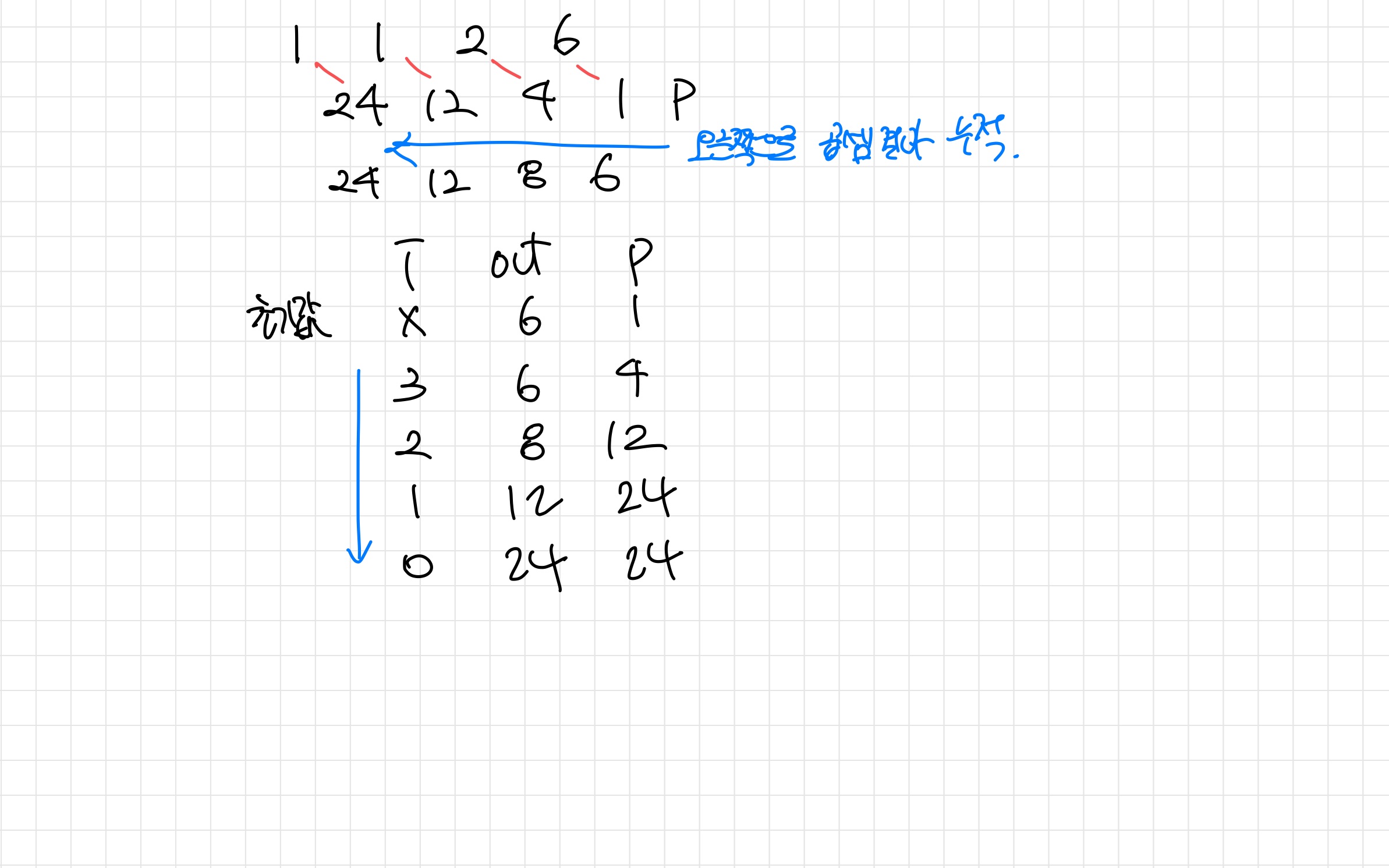
이 후 오른쪽에서 왼쪽으로 이동하여 곱셈 결과를 누적한다. 코드는 아래와 같다.
1
2
3
4
5
6
p = 1
# 왼쪽 곱셈 결과에 오른쪽 값을 차례대로 곱셈
for i in range(len(nums) - 1, - 1, -1):
out[i] = out[i] * p
p = p * nums[i]
여기서 만약 별도의 리스트 변수를 새로 만들어 곱셈 결과를 넣으면 공간 복잡도가 O(n)이 된다. 그러나 기존 out 리스트 변수에 곱셈을 하게 되면 공간복잡도가 O(1)이 되게 되어 효율적으로 풀이가 가능하다. 아래는 i가 왼쪽으로 이동하면서 out변수와 p의 변수의 변화량이다.
전체 코드는 아래와 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
def productExceptSelf(self, nums: List[int]) -> List[int]:
out = []
p = 1
# 왼쪽 곱셈
for i in range(0, len(nums)):
out.append(p)
p = p * nums[i]
p = 1
# 왼쪽 곱셈 결과에 오른쪽 값을 차례대로 곱셈
for i in range(len(nums) - 1, 0 - 1, -1):
out[i] = out[i] * p
p = p * nums[i]
return out
정리
처음엔 O(n)으로 풀이가 쉽게 떠올리지는 않았지만 왼쪽으로 이동한 곱셈값과 오른쪽으로 이동한 곱셈값을 곱하여 풀이가 가능하다라는 것을 배웠고, 공간복잡도도 O(n)으로 풀이된다는 것도 배웠다.