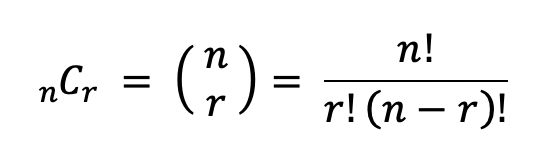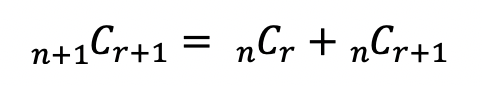이항계수란 2개의 항을 전개하여 계수를 나타낸 수를 이항계수라고 한다.
예를 들어 (a+b)^3을 전개한다고 했을 때 (a+b)^3 = a^3 + 2a^2b + 2ab^2 + b^3이 되어 계수는 {1, 3, 3, 1}이 된다. 이런식으로 이항계수들을 전개하다보면 다음과 같은 파스칼 삼각형의 모습이 나온다.
이항계수를 다르게 해석하면 b를 뽑는 개수로 이해할 수 있다.
- a^3는 b를 0개 뽑는 것
- 2a^2b는 b를 1개 뽑는 것
- 2ab^2는 b를 2개 뽑는 것
- b^3는 b를 3개 뽑는 것
이와 같이 b가 n개 있을 때 이들 중에서 r개를 뽑는 것으로 조합 공식을 이용해 이항 계수를 구할 수 있다.
즉, 이항계수를 구하려면 조합 공식을 이용해 구할 수 있고, 이를 코드로 구현하면 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
public class Combination1 {
public static void main(String[] args) {
int n = 5;
int k = 2;
System.out.println(f(n) / (f(k) * f(n - k)));
}
static int f(int n) {
if (n == 0)
return 1;
return n * f(n - 1);
}
}
위의 코드는 팩토리얼을 이용해 구한 코드다. 이렇게 구하는 방법외에도 조합의 성질을 이용해 이항계수를 알아낼 수 있다. 바로 파스칼의 법칙을 이용해 이항계수를 구할 수 있다.
위와 같은 공식을 이용해 이항계수를 구할 수 있으며 n과 r이 같거나 r = 0이면 1이 나온다는 것을 이용해 알고리즘을 작성할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
public class Combination2 {
public static void main(String[] args) {
System.out.println(combi(5, 2)); // 5C2
}
static int combi(int n, int r) {
if (n == r || r == 0) {
return 1;
}
return combi(n - 1, r - 1) + combi(n - 1, r);
}
}
위와 같이 재귀를 이용해 조합 경우의 수를 구할 수 있지만, 위는 n과 r의 숫자가 커지게 되면 재귀 형식으로 인해 스택오버플로가 발생할 수 있다. 따라서 여기에 다이나믹 프로그래밍의 핵심 아이디어인 메모리제이션을 이용해 이미 구한 조합의 경우의 수는 기록해두어 재방문하게 되면 기록한 값을 되돌려주는 방식으로 오버플로 문제를 해결할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Combination3 {
static int[][] D = new int[6][6]; // DP 테이블
public static void main(String[] args) {
System.out.println(combi(5, 2)); // 5C2
}
static int combi(int n, int r) {
if (D[n][r] > 0)
return D[n][r];
if (n == r || r == 0) {
return D[n][r] = 1;
}
return combi(n - 1, r - 1) + combi(n - 1, r);
}
}
위의 코드는 다이나믹 프로그래밍으로 풀이한 방식이며, 그 중 탑다운 방법을 이용해 구현한 것이다. 탑다운 말고도 바텀업으로도 구현이 가능해 재귀를 이용하지 않고 반복문으로 풀이도 할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Combination4 {
static int[][] D = new int[6][6];
public static void main(String[] args) {
for (int i = 0; i <= 5; i++) {
D[i][1] = i;
D[i][0] = 1;
D[i][i] = 1;
}
for (int i = 2; i <= 5; i++) {
for (int j = 1; j < i; j++) {
D[i][j] = D[i - 1][j] + D[i - 1][j - 1]; // nCr = n-1Cr-1 + n-1Cr
}
}
System.out.println(D[5][2]);
}
}
정리
이항계수를 구하는 알고리즘을 공부하다가 조합의 공식과 성질을 이용해 다양한 방식으로 알아낼 수 있어 해결하는 방법을 정리해봤다. 재귀 형식으로 구현한 코드는 입력이 극한으로 커지게 되면 스택 오버플로가 발생하게 되고, 이를 방지하기 위해 다이나믹 프로그래밍의 메모리제이션을 이용해 해결할 수 있다. 또한 스택 오버플로 방지를 위해 탑다운 방식이 아닌 바텀업 방식으로 반복문을 사용해 구현할 수 있는 것을 확인해봤다.