문제
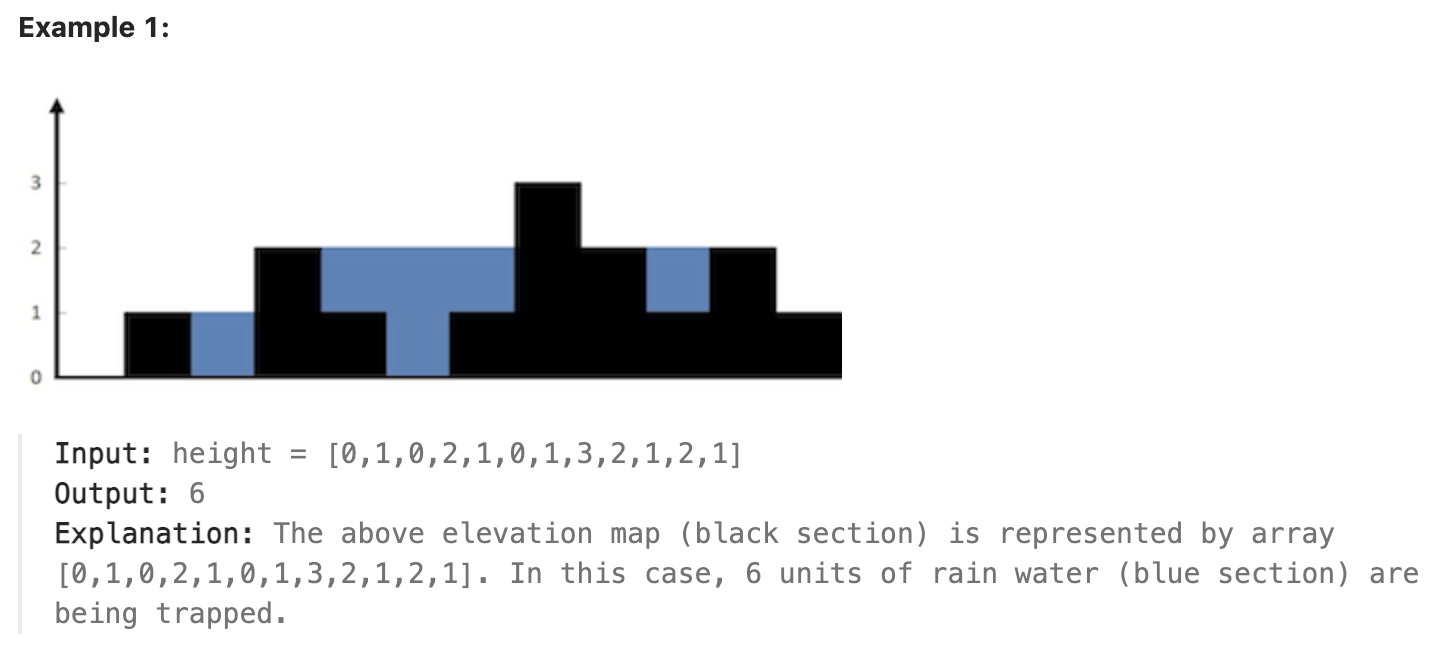
높이를 입력받아 비 온 후 얼마나 많은 물이 쌓일 수 있는지 계산하라.
입력
1
[0,1,0,2,1,0,1,3,2,1,2,1]
출력
1
6
풀이 1 (투포인터 이용)
이 문제는 투포인터를 이용하여 풀이가 가능하다.
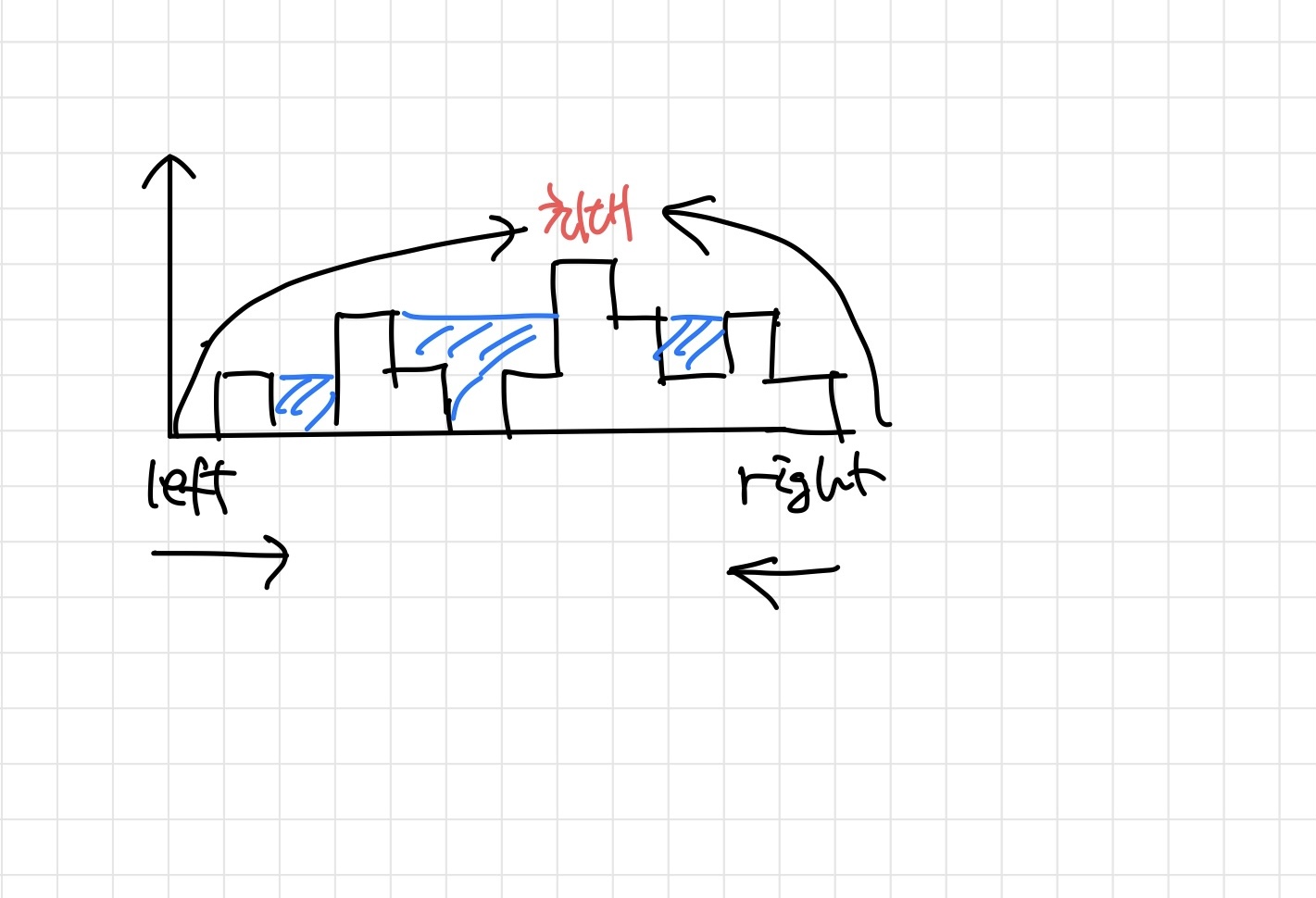
왼쪽에서 출발하는 왼쪽 포인터와 오른쪽에서 출발하는 오른쪽 포인터를 두고, 최대 높이 지점까지 가운데로 이동한다. 포인터들이 이동하면서 최대높이를 기록해놓고, 현재 포인터 위치의 높이와 비교하여 그 차이를 volume변수에 저장하여 기록해나간다. 그 코드는 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 빗물의 양을 저장하는 변수
volume = 0
# 왼쪽 포인터와 오른쪽 포인터
left, right = 0, len(height) - 1
# 이동하면서 최대높이를 기록하는 변수 left_max, right_max
left_max, right_max = height[left], height[right]
while left < right:
left_max, right_max = max(height[left], left_max), max(height[right], right_max)
# 더 높은 쪽을 향해 투 포인터 이동
if left_max <= right_max:
volume += left_max - height[left]
left += 1
else:
volume += right_max - height[right]
right -= 1
while문을 돌면서 두개의 포인터가 최대지점에서 만날때 까지 높이가 낮은쪽에서 높은쪽으로 이동해 나간다. 아래 표를 보면 포인터 두개가 이동하면서 이동하면서 기록한 최대 높이(left_max, right_max)와 빗물의 양(volume) 값의 변화다.
위와 같이 이동하여 좌우 포인터는 최대지점에서 만나게 되며, 시간 복잡도는 O(n)이 된다.
전체코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def trap(self, height: List[int]) -> int:
if not height:
return 0
volume = 0
left, right = 0, len(height) - 1
left_max, right_max = height[left], height[right]
while left < right:
left_max, right_max = max(height[left], left_max), max(height[right], right_max)
if left_max <= right_max:
volume += left_max - height[left]
left += 1
else:
volume += right_max - height[right]
right -= 1
return volume
풀이 2 (스택 쌓기)
스택을 이용하여 풀이는 스택에 높이를 삽입하면서 만약 현재 높이가 이전 높이보다 높을 때 그 격차 만큼 물높이 volume 변수에 기록해나간다. volume은 가로(distance), 세로(waters)의 길이를 곱해서 volume 변수에 계속 더해나간다. volume과 이에 해당하는 변수들의 변화량은 다음과 같다.
전체코드는 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def trap(self, height: List[int]) -> int:
stack = []
volume = 0
for i in range(len(height)):
# 변곡점을 만나는 경우
while stack and height[i] > height[stack[-1]]:
# 스택에서 꺼낸다
top = stack.pop()
# 스택이 비어있는 경우 break -> 이전에 벽이 없기 때문에 물이 고여있지않아 측정하지 않음
if not len(stack):
break
# 이전과의 차이만큼 물 높이 처리
# 가로 길이 측정
distance = i - stack[-1] - 1
# 세로 길이 측정(현재 높이와 스택에서의 높이 중 작은 값을 선택해 이전의 높이와 차를 구함)
waters = min(height[i], height[stack[-1]]) - height[top]
# 가로 X 높이 = 물의 양
volume += distance * waters
stack.append(i)
return volume
스택으로 코드를 구현하면 while문 안에서 이전 항목들을 되돌아보며 체크하기는 하지만, 전체 수행은 한번만 하기 때문에 시간복잡도는 O(n)에 풀이가 가능하다.
정리
두가지 풀이 방법으로 모두 풀어보았고, 시간복잡도는 모두 O(n)이 나오게 됐다. 코드이해가 상당히 어려웠지만 차근차근 수행과정을 살펴보니 이해되었다.